The Philosophy of Mathematics - Plato to Modern Times
The journey of mathematical philosophy is a fascinating one, stretching from the ancient ideals of Plato to the intricate theories of modern thinkers. Mathematics is not just a collection of numbers and formulas; it is a profound reflection of reality itself, a language that describes the universe. It serves as a bridge connecting the abstract world of ideas with the tangible world we experience. But how did we get here? What were the pivotal moments that shaped our understanding of mathematics? In this article, we will explore these questions, diving deep into the thoughts and contributions of significant figures throughout history.
Plato, the ancient Greek philosopher, viewed mathematics as a crucial pathway to grasping the eternal forms, the perfect and unchanging ideals that exist beyond our physical reality. He believed that through mathematics, one could achieve a deeper understanding of the world and the truths that govern it. To Plato, numbers and geometric shapes were not mere tools for calculations; they were the very essence of reality, encapsulating the fundamental properties of existence. His assertion that "the universe is written in the language of mathematics" resonates even today, underscoring the importance he placed on this discipline.
Fast forward to the time of Euclid, often referred to as the "Father of Geometry." His work, particularly the Elements, established geometry as a rigorous discipline grounded in logical reasoning. Euclid introduced an axiomatic approach, where he laid down a set of axioms and postulates from which all geometric truths could be derived. This method not only revolutionized geometry but also set a standard for mathematical proofs that persists to this day. Imagine a world where every mathematical concept is built on a solid foundation—this is the legacy of Euclid.
The axiomatic method introduced by Euclid is a cornerstone of mathematical reasoning. It emphasizes the importance of starting from accepted truths, or axioms, and logically deriving further truths from them. This approach has profound implications for how we understand mathematical truth. It raises questions such as: What constitutes an axiom? Are there universal truths in mathematics? These inquiries have sparked philosophical debates that continue to this day, challenging our perceptions of what is real and what is merely a construct.
As we delve deeper into the axiomatic method, we uncover its implications for our understanding of mathematical truth. For instance, consider the famous Euclidean parallel postulate, which states that through a point not on a line, there is exactly one parallel line that can be drawn. This seemingly simple statement has led to a plethora of philosophical discussions regarding the nature of mathematical reality. Are these truths absolute, or do they depend on the system in which they are situated? The exploration of these questions reveals the intricate relationship between mathematics and philosophy.
As mathematicians began to explore beyond Euclid's framework, non-Euclidean geometries emerged, challenging the traditional views of mathematics. In non-Euclidean geometry, the parallel postulate does not hold; instead, multiple parallel lines can exist through a single point. This radical shift not only expanded the boundaries of mathematical thought but also opened up new philosophical avenues. It prompted thinkers to reconsider the nature of space and reality itself, illustrating how mathematics can evolve and adapt in response to new ideas.
Moving into the 17th century, René Descartes introduced a groundbreaking concept: coordinate systems. By merging algebra with geometry, he created a new way to represent mathematical relationships. This fusion allowed for a more dynamic understanding of mathematical principles. Descartes' work laid the groundwork for analytic geometry, which has profound implications for both mathematics and philosophy. It raises questions about the nature of mathematical representation and how we perceive the world through a mathematical lens.
The Enlightenment era marked a significant turning point in the philosophy of mathematics. Thinkers like Leibniz and Newton made groundbreaking contributions that shaped our understanding of the discipline. Their work not only advanced mathematical thought but also influenced the broader philosophical landscape of the time. As we explore their contributions, we begin to see how mathematics became intertwined with the natural sciences, leading to a more comprehensive understanding of the universe.
Gottfried Wilhelm Leibniz's development of calculus ignited a debate that would resonate through the ages. His exploration of change and continuity raised profound philosophical questions about the nature of reality. What does it mean for something to change? How do we quantify motion? These inquiries not only advanced mathematical concepts but also forced philosophers to confront the complexities of existence itself. Leibniz's work serves as a reminder that mathematics is not just about numbers; it is a reflection of the dynamic nature of the universe.
Isaac Newton's Principia Mathematica laid the groundwork for modern physics and mathematics. His principles illustrated how mathematical laws govern the natural world, providing a framework for understanding motion and forces. Newton's work emphasized the relationship between mathematics and the physical universe, demonstrating that mathematical truths have real-world applications. This connection between abstract thought and tangible reality continues to influence mathematical philosophy, reminding us that mathematics is not just theoretical; it is a tool for understanding the universe around us.
- What is the significance of Plato's views on mathematics? Plato believed that mathematics was a pathway to understanding the eternal forms, influencing how we perceive mathematical truths.
- How did Euclid's work impact mathematics? Euclid established geometry as a rigorous discipline through his axiomatic approach, setting a standard for mathematical proofs.
- What are the implications of non-Euclidean geometry? Non-Euclidean geometries challenged traditional views and expanded the philosophical landscape of mathematics.
- How did the Enlightenment change mathematical philosophy? The Enlightenment brought significant advancements, with thinkers like Leibniz and Newton intertwining mathematics with the natural sciences.

Plato's Mathematical Ideals
Plato, one of the most influential philosophers in Western thought, regarded mathematics as a crucial pathway to understanding the eternal forms or ideals that underpin reality. His belief was that the material world is merely a shadow of a higher reality, and mathematics serves as a bridge to that realm of pure forms. For Plato, numbers and geometric shapes were not just abstract concepts; they were the very essence of truth and beauty. This perspective laid the groundwork for centuries of philosophical inquiry into the nature of mathematical truth.
In his dialogues, particularly in "The Republic," Plato emphasized the importance of education in mathematics as a means of preparing the mind for philosophical thought. He famously stated, "The beginning of wisdom is the definition of terms," which highlights his belief that clear understanding of mathematical concepts is essential for grasping deeper philosophical ideas. Plato's mathematical ideals are not merely about computations or solving equations; they are about the quest for knowledge and the pursuit of an understanding that transcends the physical world.
One of the key aspects of Plato's philosophy is his theory of forms. He posited that everything in the physical world is a reflection of these perfect forms, which exist in a non-material realm. This notion can be illustrated through the concept of a triangle. While we can draw many different triangles, each with varying angles and lengths, they all share the inherent properties of "triangularity" that exist in the realm of forms. Thus, mathematics, in Plato's view, is a way to access these immutable truths. This perspective has profound implications for how we think about mathematical reality:
- Mathematics as a Universal Language: Plato believed that mathematical truths are universal and unchanging, transcending cultural and temporal boundaries.
- Connection to Reality: According to Plato, engaging with mathematics allows us to glimpse the true nature of reality, moving beyond mere sensory experience.
- Education and Philosophy: For Plato, studying mathematics was essential for anyone seeking to become a philosopher, as it trains the mind to think logically and abstractly.
Furthermore, Plato's influence extended beyond his lifetime, inspiring future mathematicians and philosophers to explore the relationship between mathematics and reality. His ideas set the stage for later developments in mathematical philosophy, prompting thinkers to question what constitutes mathematical truth and how it relates to the physical world. The interplay between mathematical concepts and philosophical inquiry became a hallmark of Western thought, leading to rich discussions that continue to this day.
In conclusion, Plato's mathematical ideals represent a profound understanding of the role that mathematics plays in our quest for knowledge. By viewing mathematics as a means to access higher truths, Plato not only shaped the philosophical foundations of mathematics but also inspired generations of thinkers to explore the intricate relationship between mathematics and reality. As we delve deeper into the history of mathematical philosophy, we see how these early ideas laid the groundwork for the complex discussions that would follow in the centuries to come.
- What did Plato believe about the nature of mathematics? Plato believed that mathematics was a pathway to understanding eternal forms and truths that exist beyond the physical world.
- How did Plato influence later mathematical thought? His ideas about the universality of mathematical truths and the importance of education in mathematics inspired future philosophers and mathematicians.
- What is the significance of Plato's theory of forms in mathematics? Plato's theory of forms posits that mathematical concepts exist in a non-material realm, influencing our understanding of mathematical reality.

Euclid and the Foundations of Geometry
When we think about geometry, the name Euclid often springs to mind. Known as the "Father of Geometry," Euclid's work laid the groundwork for a systematic approach to mathematical reasoning that still influences us today. His seminal text, The Elements, is not just a collection of geometric propositions; it is a profound exploration of the nature of mathematical truth and logic. Imagine a world where every geometric figure is built upon a foundation of clear, unassailable truths—this was Euclid's vision.
Euclid's approach was revolutionary for its time. He introduced the concept of an axiomatic system, where a small set of self-evident truths, or axioms, serve as the starting points for deriving more complex propositions. This method not only provided a rigorous structure for geometry but also established a template for mathematical reasoning across disciplines. Think of it as constructing a building: without a solid foundation, the entire structure is at risk of collapsing. Euclid ensured that every theorem was meticulously proven based on these foundational axioms.
The axiomatic method is a cornerstone of Euclidean geometry. It consists of defining a few basic terms and establishing a set of axioms, from which all other geometric truths can be derived. For example, consider the following axioms:
- A straight line can be drawn from any point to any other point.
- A finite straight line can be extended continuously in a straight line.
- All right angles are equal to one another.
These axioms may seem simple, but they form the bedrock upon which Euclid constructed an entire universe of geometric knowledge. Through logical deduction, he derived propositions about triangles, circles, and other shapes, creating a comprehensive framework that mathematicians still refer to today.
Euclid’s axiomatic method raised profound questions about the nature of mathematical truth. If mathematical truths can be derived from a set of axioms, what does that say about the nature of reality? Are these truths merely human constructs, or do they exist independently of our understanding? Philosophers have debated these questions for centuries, and Euclid’s work serves as a pivotal reference point in these discussions. The implications of his method extend beyond geometry; they challenge us to think critically about the foundations of all mathematics.
As Euclidean geometry established itself as the dominant framework for centuries, it also set the stage for revolutionary developments in mathematical thought. The emergence of non-Euclidean geometry in the 19th century challenged the very principles that Euclid had laid out. Mathematicians like Gauss, Bolyai, and Lobachevsky explored geometries where the parallel postulate—one of Euclid's key axioms—did not hold. This was akin to opening a door to a new dimension of mathematical reality, where the familiar rules of Euclidean space no longer applied.
In non-Euclidean systems, the implications of geometry could be vastly different. For instance, in hyperbolic geometry, through a point not on a given line, there are infinitely many lines that do not intersect the original line. This discovery not only expanded the philosophical landscape of mathematics but also had profound implications for the understanding of space in physics, particularly in the context of Einstein's theory of relativity. The evolution from Euclidean to non-Euclidean geometry illustrates how mathematical philosophy is not static; it evolves and grows as new ideas challenge the established norms.
Building on Euclid’s foundations, the work of René Descartes brought a new twist to the tale. By introducing coordinate systems, Descartes effectively merged algebra with geometry, creating what we now call analytic geometry. This revolutionary approach allowed mathematicians to represent geometric shapes using algebraic equations, bridging the gap between two seemingly disparate fields. Imagine being able to describe a circle not just with a compass and straightedge but with an equation—this was a game-changer!
In summary, Euclid's contributions to the foundations of geometry are monumental. His axiomatic method not only provided a rigorous framework for geometric reasoning but also opened up philosophical inquiries that resonate to this day. The journey from Euclidean to non-Euclidean geometry showcases the dynamic nature of mathematical thought, a testament to the ever-evolving quest for understanding the universe through numbers and shapes.
- What is Euclidean geometry? Euclidean geometry is the study of plane and solid figures based on the axioms and theorems formulated by Euclid.
- Why is Euclid important in mathematics? Euclid's work laid the groundwork for modern geometry and introduced the axiomatic method, which is fundamental to mathematical reasoning.
- What is non-Euclidean geometry? Non-Euclidean geometry refers to any geometry that is based on axioms or postulates that differ from those of Euclidean geometry, particularly regarding the parallel postulate.

The Axiomatic Method
The axiomatic method is a cornerstone of mathematical reasoning that has shaped the way we understand mathematics today. Introduced by Euclid in his seminal work, the Elements, this method provides a structured framework for building mathematical theories. At its core, the axiomatic method is about starting from a set of self-evident truths—known as axioms—and deriving further truths through logical reasoning. This approach not only lends clarity to mathematical arguments but also ensures that the conclusions drawn are both rigorous and reliable.
Imagine constructing a house. You wouldn't start building the roof before laying a solid foundation, right? Similarly, in mathematics, the axiomatic method establishes a robust foundation upon which the entire structure of mathematical knowledge is built. The beauty of this method lies in its simplicity: from a few basic premises, one can explore an infinite realm of mathematical concepts and relationships. Axioms are like the seeds of a tree; they may seem small and simple, but they grow into a vast network of branches and leaves, representing the myriad of theorems and discoveries that follow.
One of the most significant implications of the axiomatic method is its role in defining mathematical truth. By relying on a set of axioms, mathematicians can engage in debates about what constitutes truth in mathematics. For instance, in Euclidean geometry, the parallel postulate serves as a critical axiom. The acceptance or rejection of this axiom leads to entirely different geometrical frameworks: Euclidean versus non-Euclidean geometries. This divergence raises profound philosophical questions: Are mathematical truths universal, or are they contingent upon the axioms we choose to accept?
Moreover, the axiomatic method has paved the way for the formalization of mathematics. In the 20th century, mathematicians like David Hilbert sought to establish a complete and consistent set of axioms for all of mathematics. Hilbert's program aimed to prove that every mathematical statement could be derived from a finite set of axioms, thereby reinforcing the idea that mathematics is a logical and systematic discipline. However, this ambition faced challenges, most notably through Kurt Gödel's incompleteness theorems, which revealed that no system of axioms could capture all mathematical truths. This revelation not only shook the foundations of mathematics but also sparked a renewed interest in the philosophical implications of the axiomatic method.
In summary, the axiomatic method is more than just a tool for mathematicians; it is a profound philosophical approach that challenges our understanding of truth, logic, and the very nature of mathematics itself. As we continue to explore the depths of mathematical thought, the axiomatic method remains a vital part of the conversation, inviting us to question and reflect on the principles that guide our mathematical journey.
- What is the axiomatic method? The axiomatic method is a way of structuring mathematical theories by starting from basic, self-evident truths (axioms) and deriving further truths through logical reasoning.
- Why is the axiomatic method important? It provides a clear and rigorous framework for mathematical reasoning, ensuring that conclusions are logically sound and reliable.
- How does the axiomatic method influence mathematical truth? By relying on a set of axioms, the method prompts discussions about what is considered true in mathematics, leading to different interpretations and frameworks.
- Who were some key figures in the development of the axiomatic method? Euclid is the most notable figure, but later mathematicians like David Hilbert and Kurt Gödel also made significant contributions to the understanding and implications of the method.

Implications for Mathematical Truth
When we delve into the axiomatic method pioneered by Euclid, we uncover profound implications for our understanding of mathematical truth. At its core, the axiomatic method asserts that mathematics is built upon a foundation of self-evident truths—axioms and postulates that serve as the bedrock for all subsequent reasoning. This approach raises intriguing questions: What does it mean for something to be "true" in mathematics? Are mathematical truths discovered, or are they invented? These questions have sparked debates among philosophers and mathematicians alike, leading to a rich tapestry of thought surrounding the nature of mathematical reality.
One of the most significant implications of this method is the distinction between absolute truth and relative truth. In mathematics, an absolute truth is a statement that holds universally, regardless of external circumstances. For instance, the statement "2 + 2 4" is an absolute truth within the framework of standard arithmetic. However, as we explore different mathematical systems—such as non-Euclidean geometry—we encounter truths that are relative to the axioms we accept. This realization leads us to ponder whether mathematical truths are as immutable as we once believed, or if they are contingent upon the frameworks we choose to adopt.
Moreover, the implications of the axiomatic method extend into the realm of philosophical inquiry. The very act of establishing axioms reflects a choice about what we consider foundational. For example, in the realm of set theory, the acceptance of the Axiom of Choice has led to results that challenge our intuitions about infinity and mathematical existence. This illustrates how the philosophical underpinnings of mathematics can shape the truths we derive from it. As mathematicians grapple with these foundational issues, we see a dynamic interplay between mathematical practice and philosophical perspective.
Furthermore, the axiomatic method invites scrutiny regarding the nature of mathematical proof itself. A proof is not merely a sequence of logical deductions; it is a narrative that connects our axioms to the conclusions we draw. This narrative aspect raises the question of whether mathematical truths are inherently objective or if they are subject to interpretation. For instance, the famous Gödel's Incompleteness Theorems suggest that within any sufficiently complex mathematical system, there are truths that cannot be proven using the axioms of that system. This revelation has profound implications for our understanding of mathematical truth, suggesting that the quest for certainty may always be somewhat elusive.
In summary, the implications of the axiomatic method for mathematical truth are vast and multifaceted. They challenge us to reconsider our assumptions about what constitutes truth in mathematics, prompting an ongoing dialogue between mathematical rigor and philosophical inquiry. As we navigate this complex landscape, we must remain open to the possibility that the truths we hold dear may be shaped by the very frameworks we establish.
- What is the axiomatic method? The axiomatic method is a way of establishing mathematical truths based on a set of self-evident principles or axioms.
- How does the axiomatic method influence mathematical truth? It shapes our understanding of what is considered true in mathematics, allowing for both absolute and relative truths depending on the axioms accepted.
- What are some implications of Gödel's Incompleteness Theorems? Gödel's theorems imply that in any complex mathematical system, there are truths that cannot be proven within that system, challenging our notions of certainty in mathematics.

Euclidean vs. Non-Euclidean Geometry
When we think about geometry, the first thing that often comes to mind is the familiar world of Euclidean geometry. This is the geometry we learned in school, where parallel lines never meet, and the angles of a triangle always add up to 180 degrees. It’s a world governed by the axioms established by Euclid, which serve as the bedrock for countless mathematical principles. But what happens when we step outside this well-trodden path? Enter non-Euclidean geometry, a fascinating realm that challenges our perceptions and expands our understanding of mathematical reality.
Non-Euclidean geometry emerged in the 19th century, primarily through the works of mathematicians such as János Bolyai and Nikolai Lobachevsky, who dared to question Euclid's fifth postulate, the parallel postulate. In their explorations, they discovered that by altering this postulate, they could create entirely new geometric systems. This notion is akin to discovering a new dimension in a familiar landscape; it’s both exhilarating and mind-bending!
To understand the differences better, let's break down the core distinctions between Euclidean and non-Euclidean geometries:
| Feature | Euclidean Geometry | Non-Euclidean Geometry |
|---|---|---|
| Parallel Lines | Through a point not on a line, exactly one parallel line can be drawn. | Through a point not on a line, infinitely many parallel lines can be drawn (Hyperbolic Geometry). |
| Sum of Angles in a Triangle | Always equals 180 degrees. | Can be less than 180 degrees (Hyperbolic) or more than 180 degrees (Elliptic). |
| Geometry of Space | Flat, two-dimensional plane. | Curved surfaces, such as spheres or hyperbolic planes. |
This table illustrates how the very fabric of geometric understanding shifts when we step away from Euclidean principles. Imagine walking on the surface of a sphere; the rules change dramatically. Triangles formed on this surface can have angles that exceed 180 degrees, creating a whole new set of relationships and truths. This shift not only altered the course of mathematics but also had profound implications for the fields of physics and cosmology.
Moreover, the advent of non-Euclidean geometry opened the door to revolutionary ideas in the 20th century, particularly in the realm of relativity. Albert Einstein's theories of space and time were heavily influenced by these geometric concepts, illustrating just how interconnected mathematics and the physical world can be. The implications of non-Euclidean geometry are not just academic; they resonate through the very laws that govern our universe.
In conclusion, the exploration of Euclidean versus non-Euclidean geometry is not merely a matter of comparing two systems; it’s a journey into the heart of mathematical philosophy. It challenges us to rethink our assumptions about space, reality, and the very nature of truth itself. As we continue to delve into these concepts, we find that mathematics is not just a collection of numbers and shapes, but a profound exploration of the world around us.
- What is the main difference between Euclidean and non-Euclidean geometry? The main difference lies in the treatment of parallel lines and the sum of angles in triangles, where non-Euclidean geometry allows for multiple parallel lines and variable angle sums.
- How did non-Euclidean geometry impact modern physics? Non-Euclidean geometry laid the groundwork for Einstein's theory of relativity, which describes gravity and the curvature of space-time.
- Can non-Euclidean geometry be applied in real life? Yes, non-Euclidean geometry has practical applications in fields such as navigation, architecture, and even in understanding the universe's shape.

Descartes and the Birth of Analytic Geometry
René Descartes, a name that resonates through the corridors of mathematical history, played a pivotal role in the evolution of mathematics with his introduction of analytic geometry. Imagine a world where geometry and algebra were like two distant relatives, only occasionally crossing paths at family gatherings. Descartes brought these two branches together, creating a powerful synergy that transformed how we understand shapes and spaces. By employing a coordinate system, he allowed mathematicians to express geometric shapes using algebraic equations, effectively bridging the gap between the two disciplines.
Before Descartes, geometry was primarily concerned with shapes, sizes, and the properties of space, while algebra dealt with numbers and operations. The moment Descartes introduced his Cartesian coordinate system, it was as if he had opened a door to a new dimension of understanding. This system uses two perpendicular axes (the x-axis and y-axis) to represent points in a plane, allowing for a visual representation of algebraic equations. For instance, the equation of a line can be expressed as y mx + b, where m represents the slope and b the y-intercept. This not only simplified the study of geometry but also made it more accessible to those who were more comfortable with algebra.
Descartes' work was revolutionary, but it was not without its philosophical implications. By merging algebra with geometry, he raised questions about the nature of mathematical objects. Are these objects merely abstract concepts, or do they have a tangible reality? This debate echoes through the ages, influencing thinkers long after Descartes. His approach also laid the groundwork for future mathematicians, such as Newton and Leibniz, who would further explore the connections between mathematics and the physical world.
Furthermore, Descartes' influence extended beyond mathematics into the realm of philosophy. His famous statement, "Cogito, ergo sum" (I think, therefore I am), reflects his quest for certainty and knowledge. In a similar vein, his contributions to analytic geometry sought certainty in mathematical representation. By providing a systematic way to analyze geometric problems through algebra, he not only advanced mathematics but also invited deeper philosophical inquiries into the nature of reality itself.
To illustrate the impact of Descartes' analytic geometry, consider the following table that compares traditional geometric methods with Descartes' approach:
| Aspect | Traditional Geometry | Analytic Geometry (Descartes) |
|---|---|---|
| Representation | Shapes and figures | Algebraic equations |
| Tools | Compass and straightedge | Coordinate axes |
| Problem-solving | Geometric constructions | Algebraic manipulation |
| Accessibility | Primarily for geometers | Accessible to algebraists |
In conclusion, Descartes' introduction of analytic geometry was a watershed moment in the history of mathematics. It not only facilitated a deeper understanding of geometric relationships but also prompted philosophical discussions that continue to resonate today. The fusion of algebra and geometry opened up new avenues for exploration, making mathematics a more dynamic and interconnected field. As we delve into the realms of modern mathematics, we can trace many of our foundational concepts back to this remarkable thinker, whose legacy continues to inspire and challenge us.

Mathematics in the Enlightenment
The Enlightenment era, often referred to as the Age of Reason, was a time of profound transformation in various fields, including mathematics. This period marked a shift from the medieval scholasticism to a more empirical and rational approach to understanding the world. Thinkers like Gottfried Wilhelm Leibniz and Isaac Newton emerged as pivotal figures, each contributing significantly to the philosophy of mathematics. They didn't just develop new mathematical theories; they also reshaped how we perceive the relationship between mathematics and the natural world.
Leibniz, a polymath in his own right, is best known for co-developing calculus independently of Newton. His work sparked intense debates about the fundamental nature of change and continuity. Imagine a world where the laws of motion and the behavior of objects were shrouded in mystery; Leibniz's calculus illuminated these concepts, providing a framework that allowed for the mathematical description of motion. His famous notation, including the integral sign (∫) and the 'd' for differentials, revolutionized mathematical communication. But beyond the symbols, Leibniz's philosophical inquiries raised essential questions: What does it mean for something to change? Is change an illusion, or is it a fundamental aspect of reality? These questions are still relevant today, echoing in modern philosophical discussions.
On the other hand, Newton's work, particularly in his seminal text Principia Mathematica, laid the groundwork for classical mechanics. He introduced the concept of gravitational force, which not only explained the motion of planets but also provided a mathematical framework that could be applied universally. Newton’s mathematical principles were not merely abstract constructs; they had real-world implications, allowing humanity to predict celestial events and understand physical phenomena with unprecedented accuracy. His famous laws of motion and the law of universal gravitation became cornerstones of both mathematics and physics, demonstrating the profound interconnectedness of these disciplines.
During this period, mathematics was not just a collection of techniques; it became a powerful tool for understanding the universe. The Enlightenment thinkers believed that through reason and mathematical reasoning, one could uncover the underlying principles governing nature. This belief led to the development of new branches of mathematics, including probability theory and statistics, which were essential for making sense of data and uncertainty in an increasingly complex world.
| Mathematician | Contribution | Philosophical Impact |
|---|---|---|
| Gottfried Wilhelm Leibniz | Co-development of Calculus | Questioned the nature of change and continuity |
| Isaac Newton | Principia Mathematica | Established laws of motion and universal gravitation |
This era also saw a growing emphasis on the importance of axiomatic systems and logical reasoning in mathematics. The rationalists believed that through clear definitions and logical deductions, one could arrive at mathematical truths that were universally valid. This approach laid the groundwork for future developments in mathematical philosophy, influencing later thinkers who would grapple with the implications of mathematical abstraction and its relation to reality.
In summary, the Enlightenment was a pivotal period in the philosophy of mathematics. The contributions of Leibniz and Newton not only advanced mathematical thought but also reshaped our understanding of the universe. Their ideas continue to resonate, inviting us to ponder the intricate relationship between mathematics, reality, and the nature of existence itself. As we navigate through the complexities of modern mathematics, we owe a debt of gratitude to these Enlightenment thinkers who dared to question, explore, and illuminate the world around us.
- What is the significance of calculus in mathematics?
Calculus allows us to understand and describe changes in various phenomena, making it essential for fields like physics, engineering, and economics. - How did the Enlightenment influence modern mathematics?
The Enlightenment emphasized reason and empirical evidence, leading to the development of rigorous mathematical methods that are still in use today. - What philosophical questions arose from the work of Leibniz and Newton?
Their work prompted discussions about the nature of reality, change, and the relationship between mathematics and the physical world.

Leibniz and the Calculus Debate
Gottfried Wilhelm Leibniz was a pivotal figure in the history of mathematics, particularly known for his role in the development of calculus. His innovative approach sparked a heated debate that would resonate through the ages, not just in mathematics but also in the philosophy of mathematics. Imagine a world where the very fabric of change and continuity was being questioned! Leibniz's work introduced concepts that challenged the existing paradigms and opened up a whole new realm of mathematical exploration.
At the heart of the calculus debate was the question of who truly invented calculus. Both Leibniz and Isaac Newton independently developed their own versions of calculus in the late 17th century, but their methodologies and notations differed significantly. Leibniz's notation, which includes the integral sign ∫ and the differential d, became widely adopted due to its elegance and efficiency. In contrast, Newton's approach was more geometrical and focused on limits. This divergence in thought led to a fierce rivalry, with each mathematician's supporters fiercely defending their respective heroes.
Leibniz viewed calculus as a tool for understanding the natural world, emphasizing the importance of infinitesimals—infinitely small quantities that are crucial for understanding motion and change. He posited that calculus could be used to describe not just physical phenomena, but also abstract concepts. This perspective was revolutionary and laid the groundwork for future mathematicians to explore the relationships between mathematics and the physical universe.
Furthermore, the implications of Leibniz's work extended beyond mere calculation. He believed that mathematics could provide insights into the nature of reality itself. For him, calculus was more than just a set of techniques; it was a philosophy that sought to explain the underlying principles of existence. This idea resonates with the notion that mathematics is a universal language, capable of expressing the complexities of the cosmos.
As the debate continued, it became clear that the differences between Leibniz and Newton were not merely technical but philosophical. While Newton focused on the physical applications of calculus, Leibniz was more concerned with the abstract foundations. This philosophical divide raised essential questions about the nature of mathematical truth:
- Is mathematics a discovery of universal truths, or is it a human invention?
- Can mathematical concepts exist independently of physical reality?
- What role do definitions and notations play in mathematical understanding?
These questions were not just academic; they influenced how subsequent generations of mathematicians and philosophers approached the subject. The calculus debate exemplified the ongoing struggle to reconcile mathematical theory with practical application, a theme that continues to be relevant today.
In conclusion, Leibniz's contributions to calculus were not merely technical innovations but profound philosophical statements about the nature of mathematics and its relationship to reality. His ideas continue to inspire and challenge thinkers in both mathematics and philosophy, reminding us that the quest for understanding is an ever-evolving journey. As we delve deeper into the philosophy of mathematics, we can see how Leibniz’s legacy invites us to question the very foundations of our mathematical beliefs.
- What was the main contribution of Leibniz to calculus? Leibniz developed a systematic notation for calculus and introduced the concept of infinitesimals, which are crucial for dealing with change and continuity.
- Why was the calculus debate important? The debate highlighted differing philosophical views on the nature of mathematics and its relationship to reality, influencing future mathematical thought.
- How did Leibniz's ideas differ from Newton's? While Newton focused on the physical applications of calculus, Leibniz emphasized its abstract foundations and the philosophical implications of mathematical concepts.

Newton's Mathematical Principles
Isaac Newton, a towering figure in the history of science, fundamentally transformed the landscape of mathematics with his seminal work, Principia Mathematica. Published in 1687, this groundbreaking text didn't just lay the groundwork for classical mechanics; it also introduced a new way of thinking about mathematics as a tool for understanding the natural world. Newton's approach was revolutionary, intertwining mathematical principles with physical laws, thus creating a framework that would dominate scientific thought for centuries.
At the heart of Newton's mathematical principles is the concept of calculus, which he developed concurrently with Gottfried Wilhelm Leibniz. While their methods differed, both mathematicians recognized the importance of understanding change. Newton's calculus was rooted in the idea of limits and infinitesimals, allowing him to describe motion and change in a way that had never been done before. This was a significant leap from the static geometry of Euclid, as it introduced a dynamic perspective on mathematical relationships.
Newton's laws of motion—his three fundamental principles—are a perfect illustration of how mathematics can describe physical reality. These laws state:
- First Law (Inertia): An object at rest stays at rest, and an object in motion stays in motion unless acted upon by a force.
- Second Law (Fma): The force acting on an object is equal to the mass of that object multiplied by its acceleration.
- Third Law (Action and Reaction): For every action, there is an equal and opposite reaction.
These principles not only provided a mathematical framework for understanding motion but also illustrated how mathematics can be used to predict outcomes in the physical world. Newton’s use of mathematics was not merely for calculation; it was a philosophical tool that allowed him to explore the underlying laws governing nature.
One of the most profound implications of Newton's work is the concept of mathematical modeling. By using equations to represent physical phenomena, Newton paved the way for future scientists and mathematicians to develop models that could predict the behavior of systems ranging from the motion of planets to the trajectory of a thrown ball. This shift from purely theoretical mathematics to applied mathematics marked a significant moment in the philosophy of mathematics, as it emphasized the importance of practical application.
Furthermore, Newton's influence extended beyond mathematics and physics into the realm of philosophy. His work prompted philosophers to rethink the nature of reality and the role of mathematics in understanding it. The debate over the nature of mathematical truths—whether they are discovered or invented—was reignited by Newton's findings. This philosophical inquiry continues to be a central theme in discussions about the foundations of mathematics today.
In conclusion, Isaac Newton's Principia Mathematica not only revolutionized mathematics but also reshaped our understanding of the physical universe. By merging mathematical principles with empirical observations, he created a legacy that would influence countless thinkers and shape the future of both mathematics and science. His work invites us to ponder deeper questions about the nature of reality, the role of mathematics in our understanding of the universe, and the philosophical implications of mathematical truths.
- What is the significance of Newton's Principia Mathematica?
Newton's Principia Mathematica is significant because it established the laws of motion and universal gravitation, integrating mathematics with physics and laying the groundwork for classical mechanics.
- How did Newton contribute to the development of calculus?
Newton developed calculus independently and contemporaneously with Leibniz, focusing on the concepts of limits and infinitesimals to analyze motion and change.
- What are Newton's three laws of motion?
Newton's three laws of motion describe the relationship between the motion of an object and the forces acting on it, providing a framework for understanding dynamics.
- What philosophical questions arise from Newton's work?
Newton's work raises questions about the nature of mathematical truths, whether they are discovered or invented, and how mathematics relates to our understanding of reality.
Principia Mathematica
This article explores the evolution of mathematical philosophy from Plato's ideals to contemporary interpretations, highlighting significant thinkers and their contributions to our understanding of mathematical truth and reality.
Plato viewed mathematics as a pathway to understanding the eternal forms. This section delves into how his beliefs shaped the philosophical foundations of mathematics and its connection to reality.
Euclid's work established geometry as a rigorous discipline. This section discusses his axiomatic approach and how it influenced subsequent mathematical thought and philosophy.
The axiomatic method introduced by Euclid set a standard for mathematical proofs. This subheading examines the significance of axioms and postulates in mathematical reasoning.
Exploring how the axiomatic method influences our understanding of mathematical truth, this section highlights the philosophical debates surrounding what constitutes mathematical reality.
This section contrasts Euclidean geometry with non-Euclidean systems, illustrating how these developments challenged traditional views and expanded the philosophical landscape of mathematics.
Descartes' introduction of coordinate systems revolutionized mathematics. This subheading discusses the philosophical implications of merging algebra with geometry.
The Enlightenment era brought significant advancements in mathematical thought. This section explores how philosophers like Leibniz and Newton contributed to the philosophy of mathematics during this period.
Leibniz's development of calculus sparked philosophical discussions about the nature of change and continuity. This subheading examines the implications of his work on mathematical philosophy.
Newton's laid the groundwork for modern physics and mathematics. This work is not merely a compilation of mathematical formulas and theorems; it represents a profound shift in how we understand the universe. Newton's approach combined rigorous mathematical analysis with physical observation, creating a framework that described the laws of motion and universal gravitation.
In , Newton introduced several key concepts that would forever alter the landscape of mathematics and science. For instance, he developed the notion of fluxions, which we now refer to as derivatives. This was revolutionary because it allowed for the analysis of motion and change in a way that had never been done before. The implications of this were vast, leading to advancements in both mathematics and the natural sciences.
Moreover, Newton's work emphasized the importance of mathematical models in understanding physical phenomena. By using mathematics as a language to describe the natural world, he paved the way for future scientists and mathematicians to explore complex systems and relationships. His laws of motion, articulated through mathematical equations, provided a clear and quantifiable way to predict the behavior of objects under various forces.
Additionally, the philosophical implications of Newton's work cannot be overstated. By suggesting that the universe operates according to fixed laws that can be expressed mathematically, he introduced a mechanistic view of nature. This idea sparked debates among philosophers and scientists about the nature of reality and the role of mathematics in understanding it. Questions arose such as:
- Is mathematics a discovery of universal truths, or is it merely a human invention?
- How does mathematical abstraction relate to the physical world?
- Can we truly understand the complexities of nature through mathematical equations alone?
These questions continue to resonate in contemporary discussions about the philosophy of mathematics and its relationship with the physical sciences. Newton's not only revolutionized mathematics but also laid the philosophical groundwork for future explorations into the nature of reality and truth.
- What is the significance of Principia Mathematica in mathematics?
It established a mathematical framework for understanding physical laws and introduced concepts like calculus that are fundamental to modern mathematics. - How did Newton's work influence later thinkers?
Newton's mechanistic view of the universe and mathematical modeling influenced countless scientists and philosophers, shaping modern scientific inquiry. - What role does philosophy play in mathematics?
Philosophy helps us explore the foundational questions about the nature of mathematical truth, existence, and its relationship to the physical world.
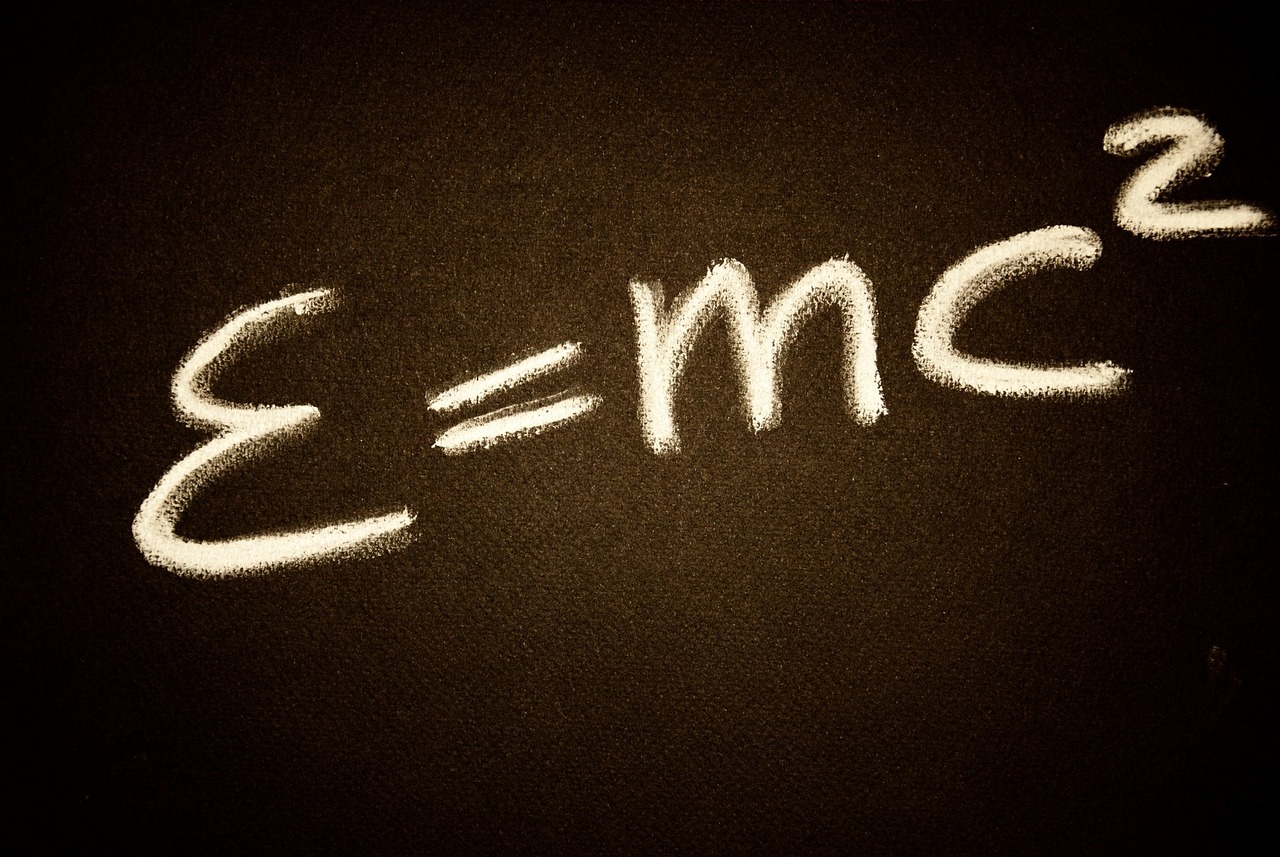
laid the groundwork for modern physics and mathematics. This section analyzes how his principles shaped the philosophical understanding of mathematical laws in nature.
Plato viewed mathematics as a pathway to understanding the eternal forms. This section delves into how his beliefs shaped the philosophical foundations of mathematics and its connection to reality.
Euclid's work established geometry as a rigorous discipline. This section discusses his axiomatic approach and how it influenced subsequent mathematical thought and philosophy.
The axiomatic method introduced by Euclid set a standard for mathematical proofs. This subheading examines the significance of axioms and postulates in mathematical reasoning.
Exploring how the axiomatic method influences our understanding of mathematical truth, this section highlights the philosophical debates surrounding what constitutes mathematical reality.
This section contrasts Euclidean geometry with non-Euclidean systems, illustrating how these developments challenged traditional views and expanded the philosophical landscape of mathematics.
Descartes' introduction of coordinate systems revolutionized mathematics. This subheading discusses the philosophical implications of merging algebra with geometry.
The Enlightenment era brought significant advancements in mathematical thought. This section explores how philosophers like Leibniz and Newton contributed to the philosophy of mathematics during this period.
Leibniz's development of calculus sparked philosophical discussions about the nature of change and continuity. This subheading examines the implications of his work on mathematical philosophy.
Newton's Principia Mathematica laid the groundwork for modern physics and mathematics. His groundbreaking work not only established the laws of motion and universal gravitation but also provided a rigorous framework for understanding the mathematical laws that govern the natural world. Newton's approach was revolutionary; he applied mathematical reasoning to physical phenomena, bridging the gap between abstract mathematics and tangible reality. This synthesis of math and physics reshaped how we perceive the universe.
In his Principia, Newton introduced the concept of calculus as a tool to describe motion and change, allowing for precise predictions of physical events. This shift in perspective led to profound philosophical inquiries about the nature of reality, causation, and the role of mathematics in explaining the universe. By viewing mathematics as a language that can articulate the laws of nature, Newton set the stage for future mathematicians and philosophers to explore the implications of mathematical truths.
Moreover, Newton's principles raised questions about the nature of mathematical laws themselves. Are they discovered or invented? Do they exist independently of the physical world, or are they merely human constructs? These inquiries continue to resonate in contemporary discussions about the philosophy of mathematics. The impact of Newton's work is evident in various fields, from physics to engineering, where mathematical principles serve as the foundation for understanding complex systems.
Overall, Newton's contributions to mathematics and physics not only advanced scientific knowledge but also enriched philosophical discourse, prompting thinkers to ponder the very essence of mathematical reality. His legacy is a testament to the power of mathematics as a tool for unlocking the secrets of the universe.
- What is the importance of Plato's philosophy in mathematics?
Plato viewed mathematics as a means to access eternal truths, influencing how later philosophers approached the subject.
- How did Euclid influence modern mathematics?
Euclid's axiomatic method laid the groundwork for logical reasoning in mathematics, shaping how proofs are constructed today.
- What is the significance of Newton's work?
Newton's Principia Mathematica integrated mathematics with physics, fundamentally altering our understanding of the natural world.
- How does the philosophy of mathematics affect modern science?
The philosophy of mathematics provides a framework for interpreting scientific theories and understanding the nature of mathematical laws.
Frequently Asked Questions
- What is the significance of Plato's philosophy in mathematics?
Plato believed that mathematics was a crucial pathway to understanding the eternal forms, or ideal realities. His philosophy laid the groundwork for viewing mathematics not just as a set of numbers and equations, but as a means to grasp deeper truths about existence and reality itself.
- How did Euclid influence modern mathematics?
Euclid's work, particularly his axiomatic approach to geometry, established a rigorous framework for mathematical proofs. This method set a standard that has influenced countless mathematicians and philosophers, making it a cornerstone of mathematical reasoning and logical deduction.
- What is the axiomatic method and why is it important?
The axiomatic method involves starting with a set of axioms or postulates and building upon them to derive further truths. This method is crucial as it provides a clear structure for mathematical reasoning, ensuring that conclusions are logically sound and based on accepted principles.
- What are the implications of Euclidean vs. Non-Euclidean geometry?
The contrast between Euclidean and Non-Euclidean geometries challenged traditional views of space and shape. Non-Euclidean systems, which emerged in the 19th century, expanded the philosophical landscape of mathematics by demonstrating that multiple geometrical realities could coexist, reshaping our understanding of mathematical truth.
- How did Descartes contribute to the philosophy of mathematics?
Descartes revolutionized mathematics by introducing the concept of coordinate systems, effectively merging algebra with geometry. This innovation not only transformed mathematical practice but also raised philosophical questions about the nature of mathematical objects and their representation in the physical world.
- What role did Leibniz play in the development of calculus?
Leibniz was pivotal in the development of calculus, which sparked intense philosophical debates about change and continuity. His ideas challenged existing notions of motion and time, influencing how we perceive mathematical functions and their applications in describing the natural world.
- How did Newton's work influence mathematical philosophy?
Newton's *Principia Mathematica* laid the foundation for modern physics and mathematics. His principles not only shaped the understanding of mathematical laws governing nature but also prompted philosophical inquiries into the relationship between mathematics and the physical universe.



















